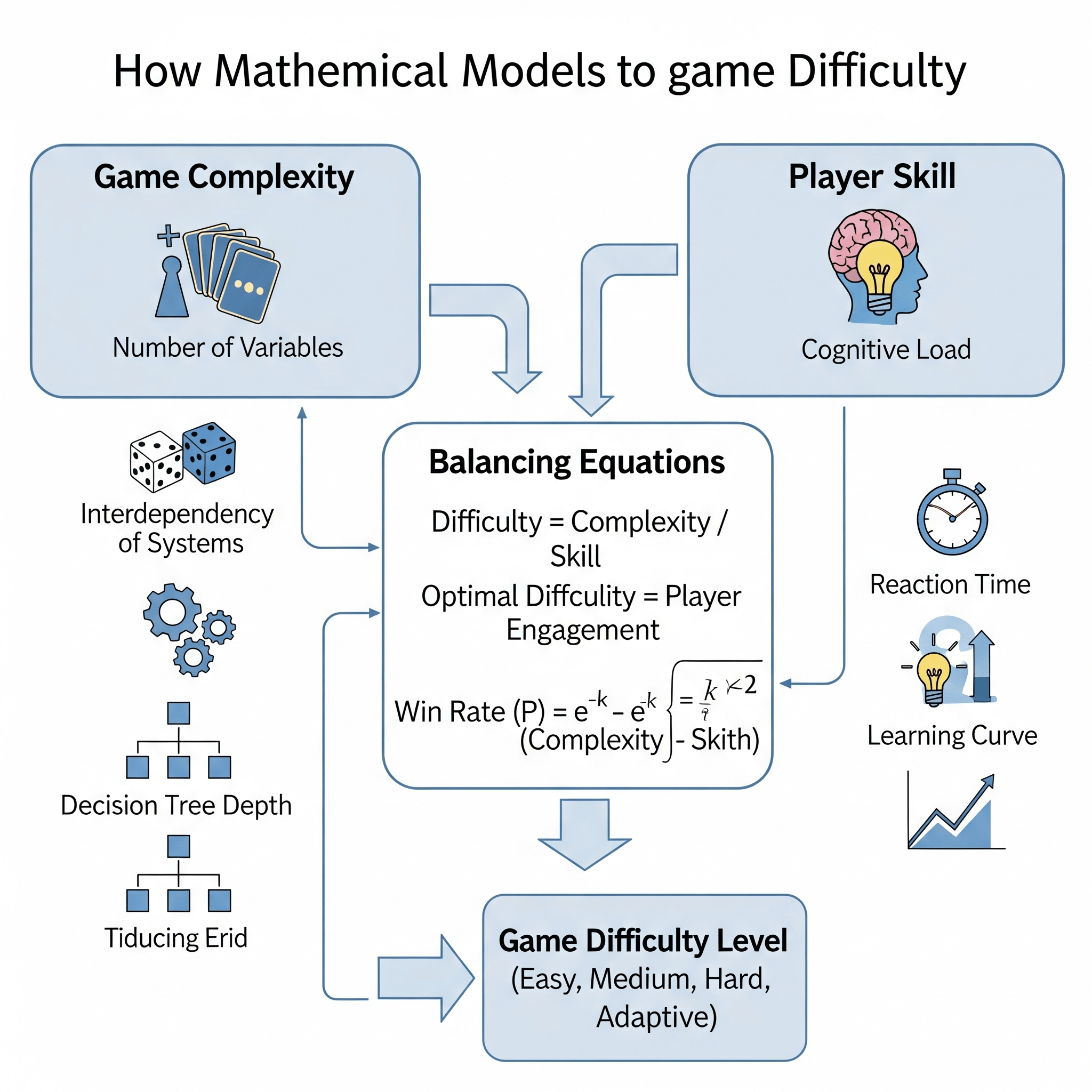
Математические модели служат невидимым фундаментом любой компьютерной игры, определяя её сложность, баланс и увлекательность. От простейших арифметических операций до сложных алгоритмов машинного обучения — математика формирует игровой опыт каждого геймера. В этой статье мы детально разберем, как различные математические подходы влияют на восприятие сложности игры, рассмотрим конкретные примеры из популярных тайтлов и поделимся практическими советами для разработчиков, стремящихся создать идеально сбалансированный геймплей.
Фундаментальные математические принципы в игровой механике
Игровая математика начинается с базовых принципов, которые кажутся простыми, но создают основу для сложных систем. Линейные модели прогрессии используются в RPG для роста характеристик персонажа, где каждый новый уровень требует фиксированного количества опыта. Такой подход обеспечивает предсказуемость развития, но может показаться однообразным опытным игрокам.
Экспоненциальные модели, напротив, создают ощущение нарастающей сложности. В играх вроде Diablo или Path of Exile стоимость улучшений растет экспоненциально, заставляя игроков принимать более взвешенные решения на поздних стадиях игры. Это математическое решение напрямую влияет на продолжительность игровых сессий и общее восприятие прогресса.
Теория вероятностей и случайность
Псевдослучайные числа формируют костяк многих игровых систем. Однако грамотные разработчики используют не чистую случайность, а управляемую рандомизацию. Например, в Dota 2 система «псевдослучайного распределения» увеличивает вероятность срабатывания критического удара с каждой неудачной попыткой, обеспечивая более предсказуемый игровой опыт.
- Равномерное распределение для базовых систем урона
- Нормальное распределение для генерации характеристик персонажей
- Экспоненциальное распределение для времени респауна ресурсов
- Биномиальное распределение для систем крафта и дропа

Алгоритмы динамической сложности и адаптивный геймплей
Современные игры используют алгоритмы машинного обучения для адаптации сложности под конкретного игрока. Left 4 Dead 2 стала пионером в использовании «AI Director» — системы, которая анализирует стиль игры команды и соответственно изменяет количество и тип противников, расположение медикаментов и оружия.
Математическая модель такой системы основана на анализе множества параметров: точность стрельбы игроков, частота использования медикаментов, время прохождения уровней, координация команды. Алгоритм строит профиль каждого игрока и подстраивает игровые события для поддержания оптимального уровня напряжения.
«Лучшая игровая математика — та, которую игрок не замечает, но чувствует её влияние на каждом шагу своего приключения»
Системы сбора данных и анализа поведения
Телеметрия игроков позволяет создавать математические модели поведения. Анализируя тепловые карты перемещения персонажей, частоту смертей в определенных локациях, популярность различных стратегий, разработчики корректируют игровой баланс с помощью статистических методов.
| Тип данных | Математическая модель | Влияние на сложность |
|---|---|---|
| Время сессии | Логнормальное распределение | Подстройка кривой прогрессии |
| Частота смертей | Пуассоновский процесс | Динамическая балансировка противников |
| Выбор стратегии | Марковские цепи | Адаптация ИИ противника |
| Социальное взаимодействие | Теория графов | Формирование команд и матчмейкинг |
Экономические модели и внутриигровые системы
Виртуальная экономика в играх строится на сложных математических моделях, которые должны обеспечивать баланс между доступностью ресурсов и их ценностью. EVE Online представляет один из самых сложных примеров игровой экономики, где цены формируются реальным спросом и предложением тысяч игроков.
Математические принципы экономического моделирования включают теорию игр для анализа взаимодействия игроков, дифференциальные уравнения для моделирования потоков ресурсов, и статистические методы для прогнозирования рыночных трендов. Разработчики используют модели инфляции и дефляции для контроля покупательной способности внутриигровой валюты.

Системы прогрессии и метагейм
Кривые роста персонажа основаны на тщательно просчитанных математических функциях. Логарифмические кривые обеспечивают быстрый прогресс на начальных этапах и замедление на высоких уровнях. Степенные функции создают равномерный рост с возможными всплесками в ключевых точках развития.
- Линейная прогрессия: простота понимания, риск однообразия
- Экспоненциальная прогрессия: нарастающая сложность, риск фрустрации
- Логарифмическая прогрессия: сбалансированный рост, естественное замедление
- S-образная кривая: реалистичное обучение, плавные переходы сложности
Искусственный интеллект и математическое моделирование поведения
ИИ противников использует сложные алгоритмы для создания убедительного игрового опыта. Конечные автоматы определяют базовое поведение, деревья решений управляют тактическим планированием, а нейронные сети обеспечивают адаптивность к стилю игры пользователя.
F.E.A.R. революционизировала игровой ИИ, используя иерархическое планирование действий (HTN) для создания впечатления разумного поведения противников. Математическая основа этой системы включает графы состояний, алгоритмы поиска пути и эвристические функции оценки ситуации.
Генетические алгоритмы в разработке игр
Некоторые разработчики используют эволюционные алгоритмы для автоматической балансировки игровых параметров. Система создает множество вариантов настроек, тестирует их на виртуальных или реальных игроках, и отбирает наиболее успешные комбинации для дальнейшего «размножения» и мутации.

Практические рекомендации для разработчиков
Создание сбалансированной математической модели требует итеративного подхода и постоянного тестирования. Начинайте с простых линейных зависимостей и постепенно усложняйте систему на основе обратной связи от игроков. Используйте A/B тестирование для сравнения различных математических подходов.
Важно помнить о психологическом восприятии чисел игроками. Урон в 127 единиц кажется более точным и реалистичным, чем ровное число 125. Прогрессия навыков должна быть интуитивно понятной — игрок должен чувствовать растущую мощь своего персонажа даже без глубокого анализа статистики.
Инструменты для математического моделирования
- Excel/Google Sheets для базовых расчетов и графиков
- Python с библиотеками NumPy и SciPy для сложных вычислений
- R для статистического анализа игровых данных
- MATLAB для инженерного моделирования физики игр
- Специализированные движки вроде Unity Analytics для сбора телеметрии
Часто задаваемые вопросы
Какие математические навыки нужны начинающему геймдизайнеру?
Базовая алгебра, понимание функций и графиков, основы статистики и теории вероятностей. Глубокое знание высшей математики не обязательно, но полезно для создания сложных систем.
Как протестировать математическую модель игры перед релизом?
Используйте симуляции с виртуальными игроками, проводите альфа и бета-тестирование с реальными пользователями, анализируйте телеметрию и корректируйте параметры на основе статистических данных.
Влияет ли сложность математической модели на производительность игры?
Да, сложные вычисления могут снижать FPS. Оптимизируйте алгоритмы, используйте кэширование результатов, выносите тяжелые расчеты в фоновые потоки или на сервер.
Можно ли использовать готовые математические библиотеки в играх?
Абсолютно! Библиотеки вроде Bullet Physics, Box2D, или математические функции Unity значительно ускоряют разработку и обеспечивают проверенную временем функциональность.
Как математические модели влияют на монетизацию игр?
Модели влияют на время удержания игроков, частоту покупок, воспринимаемую ценность внутриигровых товаров. Правильная математика может значительно увеличить доходность проекта.

Заключение: математика как основа увлекательного геймплея
Математические модели определяют не только техническую реализацию игровых механик, но и эмоциональный отклик игроков. Правильно подобранные формулы создают ощущение справедливости, прогресса и достижения. Неудачная математика может разрушить даже самую интересную игровую идею.
Современные разработчики в Казахстане и других странах СНГ активно изучают международный опыт применения математических моделей в геймдизайне. Местные студии уже создают проекты, конкурирующие с мировыми хитами благодаря грамотному использованию игровой математики.
Начинайте с изучения базовых принципов, экспериментируйте с простыми моделями, анализируйте успешные игры и не бойтесь итеративно улучшать свои математические решения. Помните: за каждым великим игровым моментом стоит точно рассчитанная формула, создающая магию интерактивного развлечения.