Каждый раз, когда вы запускаете любимую игру, за красочной графикой и захватывающим геймплеем скрывается сложная математическая система. От простых арифметических операций до продвинутых алгоритмов искусственного интеллекта — математика является фундаментом, на котором строится весь игровой опыт. В Казахстане игровая индустрия активно развивается, и понимание математических принципов игр становится всё более актуальным для разработчиков, студентов и просто любознательных геймеров.
Математика в играх — это не просто числа на экране. Это комплексная система расчётов, которая определяет физику движения персонажей, баланс игрового процесса, поведение искусственного интеллекта и даже эмоциональное воздействие на игрока. Современные игры используют математические модели такой сложности, что их изучение может стать отдельной научной дисциплиной.

В этой статье мы подробно разберём, где именно прячется математика в современных играх, как она влияет на игровой процесс и почему без неё невозможно создать по-настоящему увлекательную игру. Вы узнаете о конкретных математических концепциях, используемых в разных жанрах игр, и поймёте, как эти знания применяются на практике казахстанскими и международными разработчиками.
Основы игровой математики: От простого к сложному
Игровая математика начинается с базовых арифметических операций и постепенно усложняется до продвинутых алгоритмов. В основе любой игры лежат числовые системы, которые определяют характеристики персонажей, предметов и игрового мира в целом. Эти системы должны быть тщательно сбалансированы, чтобы обеспечить справедливый и увлекательный игровой процесс.
Одним из ключевых элементов является система прогрессии персонажа. Математические формулы определяют, сколько опыта нужно для повышения уровня, как растут характеристики и какие бонусы получает игрок. Например, популярная формула прогрессии использует экспоненциальный рост, где каждый следующий уровень требует значительно больше опыта, чем предыдущий.
Системы характеристик и их математическое обоснование
В ролевых играх математика определяет взаимодействие различных характеристик персонажа. Сила влияет на урон в ближнем бою, ловкость — на точность атак и уклонение, интеллект — на магический урон и запас маны. Каждая из этих характеристик связана с другими через сложные математические формулы, создающие многослойную систему развития персонажа.
Особенно интересно рассмотреть формулы расчёта урона. В большинстве игр базовый урон оружия умножается на коэффициент, зависящий от характеристик персонажа, затем применяются различные модификаторы — критический удар, бонусы от экипировки, временные эффекты. Итоговая формула может выглядеть как сложное математическое выражение с множественными переменными.
| Тип характеристики | Влияние на урон | Математическая формула |
|---|---|---|
| Сила | Физический урон | Базовый урон × (1 + Сила/100) |
| Интеллект | Магический урон | Магический урон × (1 + Интеллект/50) |
| Ловкость | Шанс критического удара | Базовый шанс + (Ловкость × 0.1)% |
Случайность и псевдослучайность в играх
Один из самых важных аспектов игровой математики — это управление случайностью. Истинная случайность может привести к фрустрации игроков, поэтому разработчики используют псевдослучайные системы, которые кажутся случайными, но на самом деле следуют определённым математическим закономерностям.
Например, система псевдослучайного распределения (PRD) гарантирует, что если событие с 25% вероятностью не произошло несколько раз подряд, то вероятность его наступления в следующий раз увеличивается. Это предотвращает ситуации, когда игрок может не получить критический удар десять раз подряд, что технически возможно при истинной случайности.
Геометрия и физика в игровом пространстве
Современные игры активно используют геометрические и физические принципы для создания реалистичного игрового мира. Трёхмерная геометрия определяет, как объекты располагаются в пространстве, как работают коллизии и как рассчитываются траектории движения.
Векторная математика играет ключевую роль в расчётах направления и скорости движения объектов. Каждый персонаж, снаряд или частица в игре представлен набором векторов, которые определяют его положение, скорость и ускорение в трёхмерном пространстве. Эти векторы постоянно пересчитываются в реальном времени, создавая плавное движение.

Системы коллизий и пространственная оптимизация
Для обнаружения столкновений между объектами используются различные геометрические алгоритмы. Простейший подход — проверка пересечения ограничивающих прямоугольников (bounding boxes), но для более точных расчётов применяются сложные алгоритмы проверки пересечения многоугольников и трёхмерных тел.
Пространственная оптимизация решает проблему производительности при большом количестве объектов. Алгоритмы разбиения пространства, такие как октодеревья (octrees) и BSP-деревья, позволяют быстро определить, какие объекты могут потенциально пересекаться, не проверяя все возможные комбинации. Это критически важно для игр с открытым миром, где одновременно существуют тысячи интерактивных объектов.
Физические симуляции и реалистичность движения
Современные физические движки используют законы Ньютона для создания реалистичного поведения объектов. Гравитация, трение, инерция, упругость — все эти физические свойства моделируются с помощью дифференциальных уравнений, которые решаются численными методами в реальном времени.
Особенно сложными являются расчёты деформаций мягких тел, жидкостей и газов. Для моделирования воды часто используются уравнения Навье-Стокса, описывающие движение вязких жидкостей. Хотя точное решение этих уравнений невозможно в реальном времени, разработчики используют различные приближения и упрощения для достижения визуально правдоподобного результата.
Алгоритмы искусственного интеллекта в играх
Искусственный интеллект в играх — это одна из самых математически насыщенных областей разработки. От простых конечных автоматов до сложных нейронных сетей, ИИ определяет поведение неигровых персонажей (NPC), адаптируется к стилю игры пользователя и создаёт динамичные игровые ситуации. В Казахстане всё больше разработчиков изучают продвинутые алгоритмы ИИ для создания более умных и реалистичных противников.
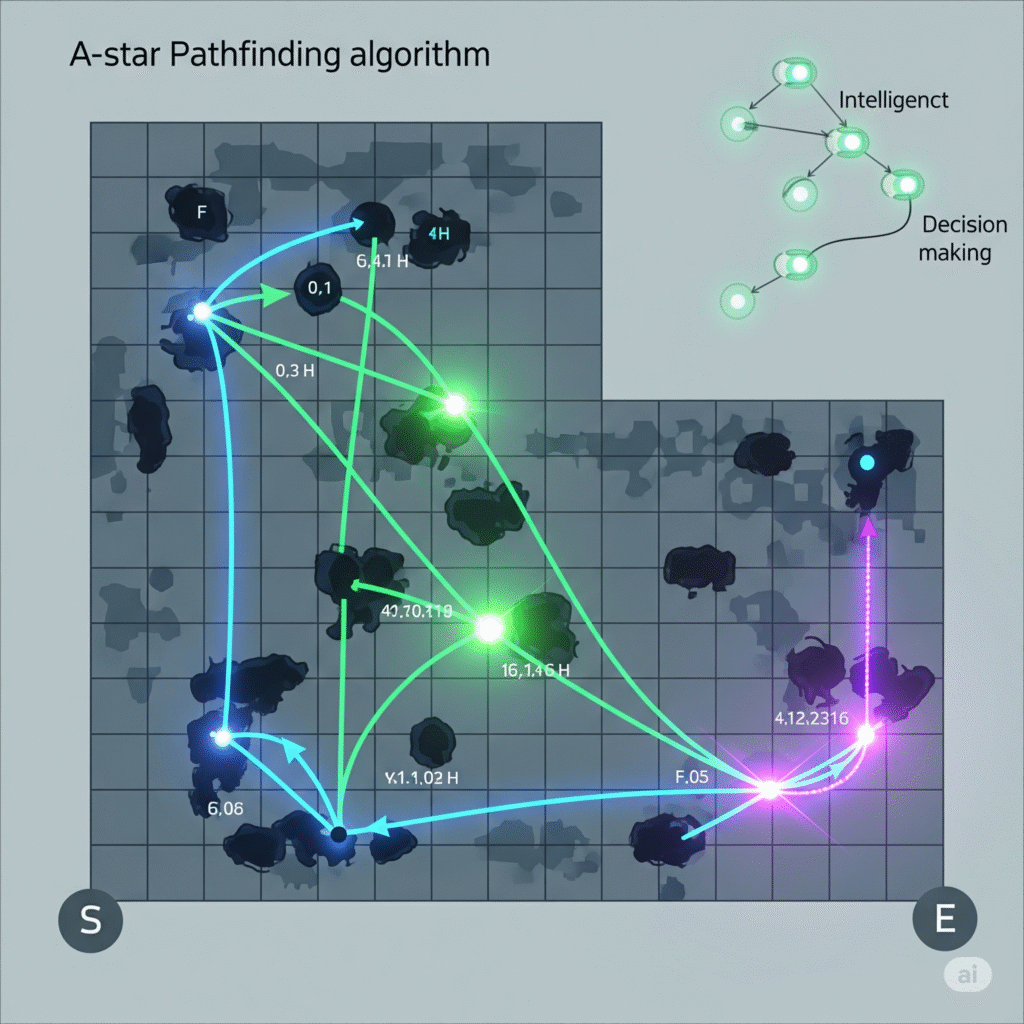
Алгоритмы поиска пути (pathfinding) используют графовые структуры данных и математические методы оптимизации. Алгоритм A* (A-звезда) является золотым стандартом в игровой индустрии благодаря своей эффективности и гарантии нахождения оптимального пути. Он использует эвристическую функцию для оценки расстояния до цели, что позволяет значительно сократить количество проверяемых узлов.
Деревья поведения и машины состояний
Современные системы ИИ в играх часто основаны на деревьях поведения (behavior trees) — иерархических структурах, которые определяют логику принятия решений персонажем. Каждый узел дерева представляет собой математическую функцию, которая возвращает одно из трёх состояний: успех, провал или выполнение. Эта система позволяет создавать сложное поведение из простых компонентов.
Конечные автоматы (finite state machines) используются для моделирования различных состояний персонажа: патрулирование, преследование, атака, отступление. Переходы между состояниями определяются математическими условиями, основанными на расстоянии до игрока, уровне здоровья, наличии боеприпасов и других параметрах. Эти условия часто представляют собой логические выражения с несколькими переменными.
Нейронные сети и машинное обучение
Современные игры всё чаще используют нейронные сети для создания адаптивного ИИ. Эти системы способны обучаться на основе действий игрока и изменять своё поведение соответственно. Математической основой нейронных сетей являются линейная алгебра и дифференциальное исчисление, используемые в алгоритмах обратного распространения ошибки.
Генетические алгоритмы применяются для эволюции поведения ИИ в играх. Каждый «ген» представляет собой параметр поведения, а «мутации» — случайные изменения этих параметров. Алгоритм отбирает наиболее успешные варианты поведения и создаёт новые поколения ИИ-агентов путём комбинирования и мутации их характеристик.
Экономические системы и теория игр
Внутриигровая экономика — это сложная математическая система, которая должна быть сбалансированной и устойчивой к инфляции. Разработчики используют экономические модели для определения стоимости предметов, скорости получения ресурсов и механизмов их расходования. Неправильно настроенная экономика может привести к дисбалансу игры и потере интереса у игроков.
Теория игр находит применение в многопользовательских играх, где игроки принимают стратегические решения, влияющие друг на друга. Концепции равновесия Нэша помогают разработчикам создавать ситуации, где ни один игрок не может улучшить свою позицию, изменив только свою стратегию. Это особенно важно для создания сбалансированного PvP-контента.
Модели ценообразования и инфляция
Математические модели ценообразования определяют, сколько должны стоить различные предметы в игре. Учитывается время, необходимое для их получения, их полезность, редкость и влияние на игровой баланс. Часто используются логарифмические функции для определения цен редких предметов, что предотвращает экспоненциальный рост стоимости.
Для борьбы с инфляцией разработчики внедряют «поглотители» игровой валюты — механизмы, которые удаляют деньги из экономики. Это могут быть налоги на торговлю, дорогостоящие улучшения экипировки или временные бонусы. Математические модели помогают определить оптимальные коэффициенты для поддержания экономического равновесия.
- Производство ресурсов: Скорость появления игровой валюты и предметов
- Потребление ресурсов: Механизмы удаления валюты из экономики
- Торговые комиссии: Процент от сделок, идущий в «никуда»
- Временные события: Специальные акции и распродажи
Графика и математические основы рендеринга
Компьютерная графика в играх полностью основана на математике. Линейная алгебра, тригонометрия и аналитическая геометрия используются для проецирования трёхмерных объектов на двумерный экран, расчёта освещения, текстурирования и создания специальных эффектов. Современные графические процессоры (GPU) по сути являются мощными математическими сопроцессорами.
Матричные преобразования лежат в основе всех операций с 3D-графикой. Перемещение, поворот и масштабирование объектов выполняются путём умножения векторов координат на соответствующие матрицы преобразования. Проекционная матрица переводит трёхмерные координаты в экранные координаты, создавая иллюзию объёмного изображения на плоском экране.
Шейдеры и программируемые графические конвейеры
Шейдеры — это небольшие программы, которые выполняются на GPU и определяют, как должны выглядеть пиксели на экране. Вершинные шейдеры обрабатывают геометрию объектов, фрагментные шейдеры определяют цвет каждого пикселя. Эти программы написаны на специализированных языках программирования и интенсивно используют математические функции и операции с векторами.
Освещение в 3D-графике моделируется с помощью различных математических моделей. Модель освещения Фонга использует скалярное произведение векторов для расчёта диффузного и зеркального отражения света. Более сложные модели, такие как physically based rendering (PBR), используют физически обоснованные формулы для создания фотореалистичного изображения.

Процедурная генерация контента
Процедурная генерация позволяет создавать огромные игровые миры с минимальными затратами на ручную работу художников. Математические алгоритмы генерируют ландшафты, города, подземелья и даже целые планеты. В основе этих алгоритмов лежат функции шума, фракталы и стохастические процессы.
Алгоритм Перлина (Perlin noise) является основой для генерации естественно выглядящих ландшафтов. Он создаёт плавные случайные значения, которые интерпретируются как высота местности. Комбинирование нескольких слоёв шума с разными частотами и амплитудами позволяет создавать сложные и реалистичные ландшафты с горами, долинами и плато.
Фрактальная геометрия в игровых мирах
Фракталы используются для создания сложных структур из простых математических формул. Береговые линии, горные хребты, облака и растительность часто генерируются с помощью фрактальных алгоритмов. Самоподобие фракталов позволяет создавать детализированные объекты на любом масштабе — от общего вида горного хребта до текстуры отдельного камня.
Клеточные автоматы применяются для генерации пещер, лабиринтов и органических структур. Эти алгоритмы начинают с простого начального состояния и применяют набор правил для каждой «клетки» игрового мира. После нескольких итераций получаются сложные и интересные структуры, которые выглядят естественно, но созданы чисто математическими методами.
«Процедурная генерация — это искусство превращения математических формул в увлекательные игровые миры. Каждая формула может стать основой для бесконечного количества уникальных локаций.» — Ведущий разработчик игровых алгоритмов
Заключение: Математика как основа игрового искусства
Математика пронизывает все аспекты современных игр — от простейших механик до сложнейших систем искусственного интеллекта. Понимание математических принципов, лежащих в основе игр, открывает новые возможности как для разработчиков, так и для игроков. В Казахстане растёт интерес к изучению игровых технологий, и знание математических основ становится ключевым навыком для будущих специалистов игровой индустрии.
Развитие игровых технологий продолжается, и математические методы становятся всё более изощрёнными. Машинное обучение, квантовые алгоритмы, нейроморфные вычисления — все эти передовые области математики и информатики находят применение в играх. Те, кто сегодня изучает математические основы игр, завтра будут создавать игровые миры нового поколения.
Часто задаваемые вопросы
Нужно ли знать математику, чтобы разрабатывать игры?
Базовые знания математики необходимы для понимания игровых механик и алгоритмов. Однако современные игровые движки предоставляют множество готовых решений, что позволяет создавать игры и без глубокого понимания сложных математических концепций.
Какие разделы математики наиболее важны для игровой разработки?
Ключевыми являются линейная алгебра (векторы и матрицы), тригонометрия, теория вероятностей и базовые знания дифференциального исчисления. Для специализированных областей могут потребоваться более глубокие знания соответствующих разделов.
Как математика влияет на игровой баланс?
Математические формулы определяют соотношение силы различных игровых элементов. Правильно настроенные формулы обеспечивают справедливую конкуренцию между различными стратегиями игры, предотвращают доминирование одной тактики над всеми остальными.
Используются ли в казахстанских играх сложные математические алгоритмы?
Да, казахстанские разработчики активно изучают и применяют передовые математические методы. Многие студии сотрудничают с местными университетами для разработки инновационных алгоритмов и внедрения новых технологий в игровые проекты.
Можно ли изучать математику через игры?
Безусловно! Многие образовательные игры специально созданы для изучения математических концепций. Кроме того, анализ механик любимых игр может стать отличным способом понять практическое применение математических принципов в реальных проектах.